Пластовое давление

Обычно прогноз пластового давления основан на предположении о том, что оно изменяется строго пропорционально глубине скважины, причем коэффициент пропорциональности называют часто коэффициентом (индексом) аномальности k_a:

p_пл = r_в gl_плk_a , (1.1)

где r_в – плотность воды, кг/м³,

l_пл– глубина расположения пласта (в наклонно направленных скважинах вместо глубины по стволу берут вертикальную проекцию ствола на данной глубине.), м.

Тогда получается, что для определения пластового давления вполне достаточно знать только величину k_a для различных интервалов бурения. Обычно принимают, что для некоторого интервала бурения k_a – величина постоянная. Однако то обстоятельство, что для всех интервалов бурения расчет пластового давления ведут с помощью формулы (1.1), представляющей собой уравнение прямой, исходящей их начала координат, означает, во-первых, что линии пластовых давлений являются отрезками прямых, а во-вторых, продолжения этих отрезков образуют лучи, исходящие из устья скважины.

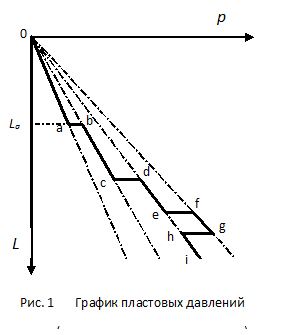
На рис. 1 показаны четыре луча, соответствующие разным значениям индекса пластового давления k_a . У луча 0а оно минимально, а у луча 0g – максимально. На глубине L_а изменяется индекс аномальности k_a , и линия скачком переходит на другой луч и так далее. В результате образуется ломаная линия 0abcdefghi, включающая горизонтальные участки ab, cd, ef, hg. Известны случаи локального роста пластового давления на некотором интервале бурения (по сравнению с соседними пластами) с последующим возвратом на прежний (или близкий к прежнему) уровень давлений. На рис. 1. этому соответствует участок efghi.

Такой упрощенный, хотя и популярный в практике проектирования скважин, метод прогнозировании пластового давления привносит в расчеты значительные ошибки, особенно в верхних интервалах разреза и при расчетах давления для пластов с аномально высоким пластовым давлением (АВПД). Но прежде чем перейти к обсуждению более точных методов прогнозирования пластовых давлений дадим определение понятия градиент пластового давления q_пли сравним его с коэффициентом аномальности k_a .

Величина q_пл, в строгом смысле, характеризует изменение пластового давления в пределах некоторого интервала бурения или пласта, приходящееся на единицу длины (как правило, это 1 м) и вычисляется по формуле:

q_пл = (p_пл2 - p_пл1)/ (L₂ - L₁), (1.2)

где p_пл2 и p_пл1 – пластовые давления соответственно на глубинах L₂и L₁ (например, в подошве и кровле пласта).

Если обнаружится, что для любых двух глубин в пределах данного интервала бурения (пласта) величина q_пл постоянна (одна и та же), то это будет означать, что пластовое давление изменяется по линейному закону.

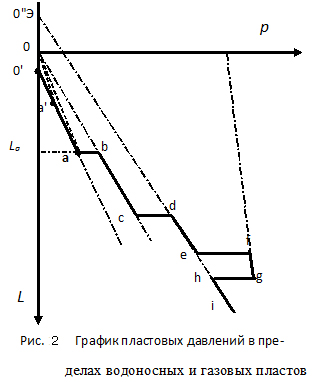
Но это совсем не означает, что продолжение прямой пройдет точно через устье скважины, как это имеет место на рис. 1. И здесь возможны варианты (рис. 2):

1. Участок 0' a отражает изменение р_пл в верхней части разреза, насыщенной пресными или маломинерализованными водами со статическим уровнем пластовой воды в скважине, как правило, ниже уровня земли ("сухой" отрезок 0-0'). Предположим теперь, что каким-то образом удалось замерить пластовые давления в точках a' и a. Вычисляя теперь по формуле (1.1) коэффициенты аномальности k_a (при известных давлениях и глубинах), мы бы получили разные величины k_a для указанных глубин (прямые 0а и 0а' не совпадают). Но выше мы только что доказали, что наличие линейной связи между давлением и глубиной автоматически означает постоянство градиента давления. В этих условиях применение формулы (1.1) с коэффициентом k_a, найденным по глубине L_a, приведет к завышению р_пл для всех глубин, меньших L_a.

2. Если продолжение прямой линии пластового давления (прямая 0 с на рис. 2) проходит через устье скважины, то имеет место частный случай постоянства k_a и q_пл на всем интервале бурения. При этом расчеты по формуле (1.1) будут тоже точными.

3. Продолжение прямой пластовых давлений может пройти и выше устья (прямая 0" е на рис. 2). Это может быть, например, в случае, когда высота области питания для данного водоносного горизонта находится намного выше того места, где бурится скважина (геологических причин формирования АВПД множество. Указанная причина - одна из возможных.). Расчет по формуле (1.1) будет отягощен ошибками, как и в случае 1, так как коэффициент аномальности, в отличие от градиента давления, будет переменным по длине интервала бурения.

4. Продуктивная толща газовых месторождений и некоторых, например, Прикаспийских, имеют большую протяженность (несколько сотен метров), и отдельные проницаемые участки (коллектора) имеют между собой гидродинамическую связь в вертикальном направлении. Такие залежи месторождений называют массивными. Пластовое давление в пределах продуктивных пластов распределяется не пропорционально глубине, а в соответствии с плотностью флюида в пластовых условиях. В продуктивной части газового месторождения – в зависимости от плотности сжатого газа, в нефтяных – от плотности нефти в пластовых условиях. На рис. 2 прямая fg иллюстрирует распределение давления в газовой залежи. Считается, что в подошве залежи давление близко к давлению в водоносных пластах на соответствующей глубине, зато в кровле оно существенно больше "нормального" и воспринимается как АВПД. Для таких случаев прогнозный расчет по формуле (1.1) в принципе возможен только для подошвы залежи. Что касается давления в кровле, то оно определяется по формулам (соответственно для газа и нефти):

p_кр = p_пд /exp[10^-4b_г(L_пд – L_кр)], (1.3)

p_кр = p_пд - r_нg(L_пд – L_кр), (1.4)

где p_пд и p_кр – пластовое давление в подошве и в кровле пласта;

b_г - относительная сжимаемость природного газа;

r_н- плотность нефти в пластовых условиях;

L_пд и L_кр - глубины расположения подошвы и кровли пласта соответственно.

Для многопластовых месторождений нефти, когда каждый нефтеносный пласт может рассматриваться как самостоятельная залежь малой мощности (единицы метров) с собственным водонефтяным контактом, в пределах нефтеносной части распределение тоже будет по закону, описанному формулой (1.4). Однако, в связи с малой мощностью пластов, описанным эффектом аномальности в кровле пренебрегают, и пластовые давления определяют либо по формуле (1.1), либо через градиент давления q_пл, если известно давление для одной из глубин в пределах рассматриваемого интервала бурения.

На линии пластовых давлений выделяются горизонтальные площадки, что свидетельствует о скачкообразном изменении пластового давления при достижении определенных глубин. Если подходить формально, то получается, что в одной точке пласта существуют два давления, что абсурдно. Все дело в том, что в реалии переход от одного давления к другому происходит не сразу, а на некотором, относительно коротком (в несколько метров) интервале. Вследствие малости интервала переход на новое давление показывают в виде ступенек.

Существует еще один способ оценки пластового давления и его изменения, суть которого сводится к определению эквивалентной плотности жидкости, которая, находясь (условно) в скважине от рассматриваемой точки пласта на глубине L_i до устья, создает гидростатическое давление, численно равное пластовому на данной глубине:

r_экв = р_пл.i /(L_i g) (1.5)

Понятие "эквивалентная плотность" применяется не только к пластовому давлению, но используется и для описания всех других давлений, представленных в ТПД: гидростатического, давления гидроразрыва и горного. Вычисляются они по формуле (1.5) с заменой числителя на значения соответствующих давлений.

А теперь сравним размерности и величины параметров k_a , q_пл , r_экв , которые служат исключительно для оценки уровня давлений и их изменения с глубиной скважины.

Из формулы (1.1) следует, что коэффициент k_a - величина безразмерная. Он призван показать, во сколько раз пластовое давление превышает давление столба воды на той же глубине в предположении, что скважина полностью ею заполнена (условно, конечно). Нередко величина k_a превышает 1,8, что требует применения утяжеленных растворов соответствующей плотности.

Предположим, что в кровле пласта на глубине 2000 м пластовое давление оказалось равным 21,6 МПа, а в подошве, на глубине 2500 м – 27 МПа.

Тогда:

- коэффициент аномальности k_a = 21,6*10⁶/ (1000*9,81*2000)=1,1 (на глубине 2000 м),

- коэффициент аномальности k_a = 27*10⁶/ (1000*9,81*2500)=1,1 (на глубине 2500 м),

- градиент пластового давления в интервале 2000-2500 м:
q_пл = (27-21,6)/ (2500-2000) = 0,0108 МПа/м,

- эквивалентная плотность по пластовому давлению на глубине 2500 м:
r_экв = 27*10⁶/ (9,81*2500) = 1100 кг/м³.

По величинам k_a иr_экв можно заключить, что пластовые давления в указанном интервале на 10 % превышают давление воды с плотностью 1000 кг/м ³.

Обобщим изложенное:

Приближенный, но весьма распространенный метод прогнозирования пластового давления, предполагает использование формулы (1.1).

Более строгий метод расчета пластового давления предусматривает точное знание давления на одной из глубин в пределах пласта (интервала бурения), например, прямым измерением глубинными манометрами, и расчет давления для других глубин с использованием величины градиента давления(По определению пластовое давление – фактор природный, и его величина в принципе не может зависеть от человека. Однако бывает пластовое давление "рукотворным". Например, в результате добычи нефти имеет место уменьшение давления в продуктивных пластах. При закачке в пласт жидкости или газа для восстановления пластовой энергии оно, наоборот, увеличивается и может превысить первоначальное давление. ).

Изменение пластового давления в зависимости от глубины можно отобразить с помощью графика "глубина - эквивалентная плотность".